June 2022
Single Cell RNAseq Analysis Workflow
Why do high-dimensional data pose a problem?
- Single cell analysis is aimed at cluster the cells according to their gene expression
- Thousands of genes across the cells
- Problem with high-dimensional data
- Human intuition and understanding is limited to a three dimensional world
- As we increase the number of Dimensions, our data becomes more sparse. The average distance in between two points of our data set is increased and invariant.
There are many dimensionality reduction algorithms
Which genes should we use for downstream analysis?
We want to select genes that contain biologically meaningful variation, while reducing the number of genes which only contribute with technical noise
We can model the gene-variance relationship across all genes to define a data-driven “technical variation threshold”
From this we can select highly variable genes (HVGs) for downstream analysis (e.g. PCA and clustering)
Principal Components Analysis (PCA)

It’s a linear algebraic method of dimensionality reduction
Finds principal components (PCs) of the data
- Directions where the data is most spread out (highest variance)
- PC1 explains most of the variance in the data, then PC2, PC3, etc.
- PCA is primarily a dimension reduction technique, but it is also useful for visuvalization
- A good separation of dissimilar objects is provided
- Preserves the global data structure
Principal Components Analysis (PCA)

When data is very highly-dimensional, we can select the most important PCs only, and use them for downstream analysis (e.g. clustering cells)
This reduces the dimensionality of the data from ~20,000 genes to maybe 10-20 PCs
Each PC represents a robust ‘metagene’ that combines information across a correlated gene set
Prior to PCA we scale the data so that genes have equal weight in downstream analysis and highly expressed genes don’t dominate
How many principal components for downstream analysis?
After performing PCA we are still left with as many dimensions in our data as we started
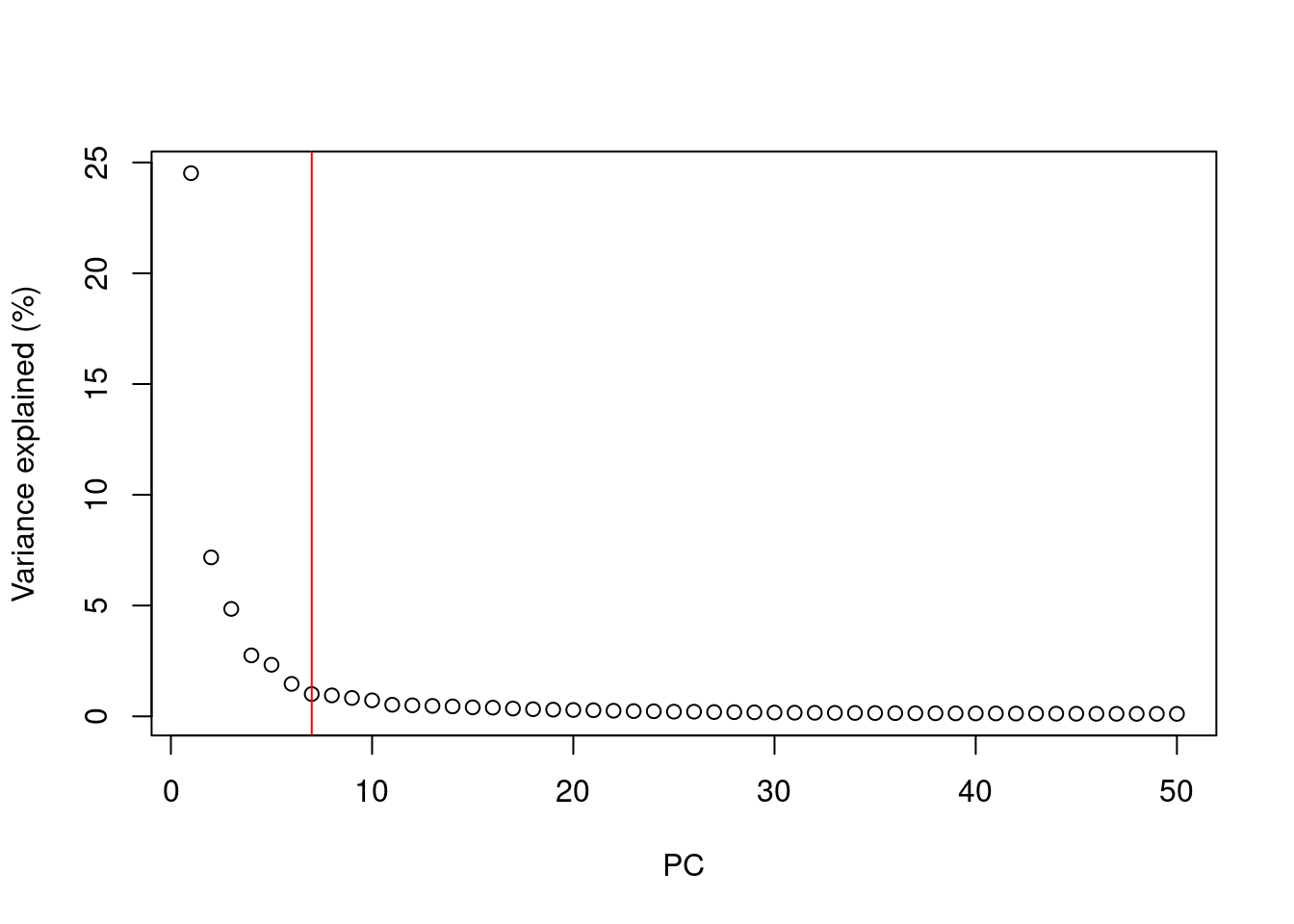
But our principal components progressively capture less variation in the data
How do we select the number of PCs to retain for downstream analysis?
Using the “Elbow” method on the scree plot
Using the model of technical noise (shown earlier)
Trying downstream analysis with different number of PCs (10, 20, or even 50)
Visualizing PCA results: PC scores
Because PC1 and PC2 capture most of the variance of the data, it is common to visualise the data projected onto those two new dimensions.
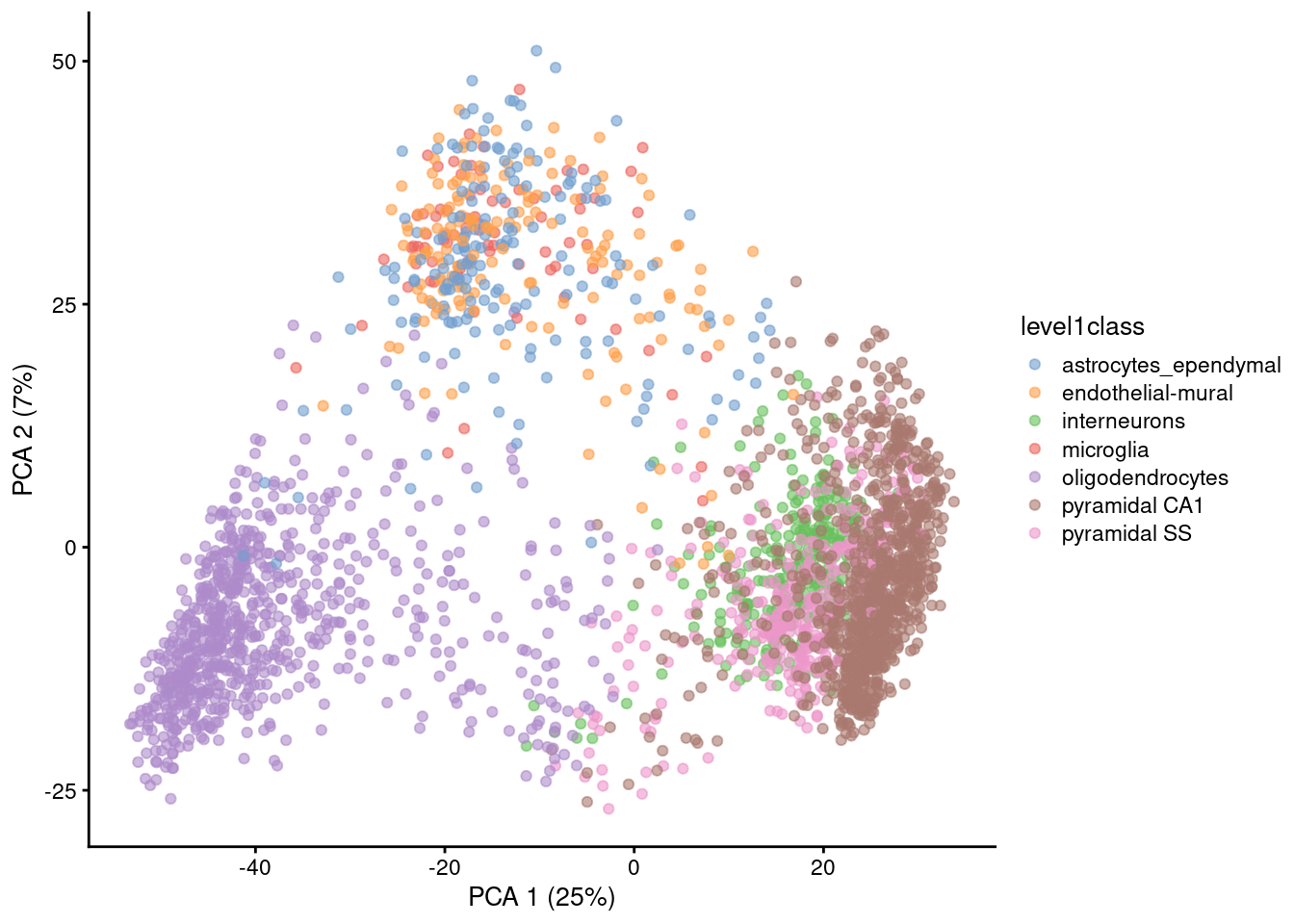
Gene expression patterns will be captured by PCs -> PCA can separate cell types
Note that PCA can also capture other things, like sequencing depth or cell heterogeneity/complexity!
Other dimensionality reduction methods
Graph-based, non-linear methods: UMAP and t-SNE
These methods can run on the output of the PCA, which speeds their computation and can make the results more robust to noise
t-SNE and UMAP should only be used for visualisation, not as input for downstream analysis
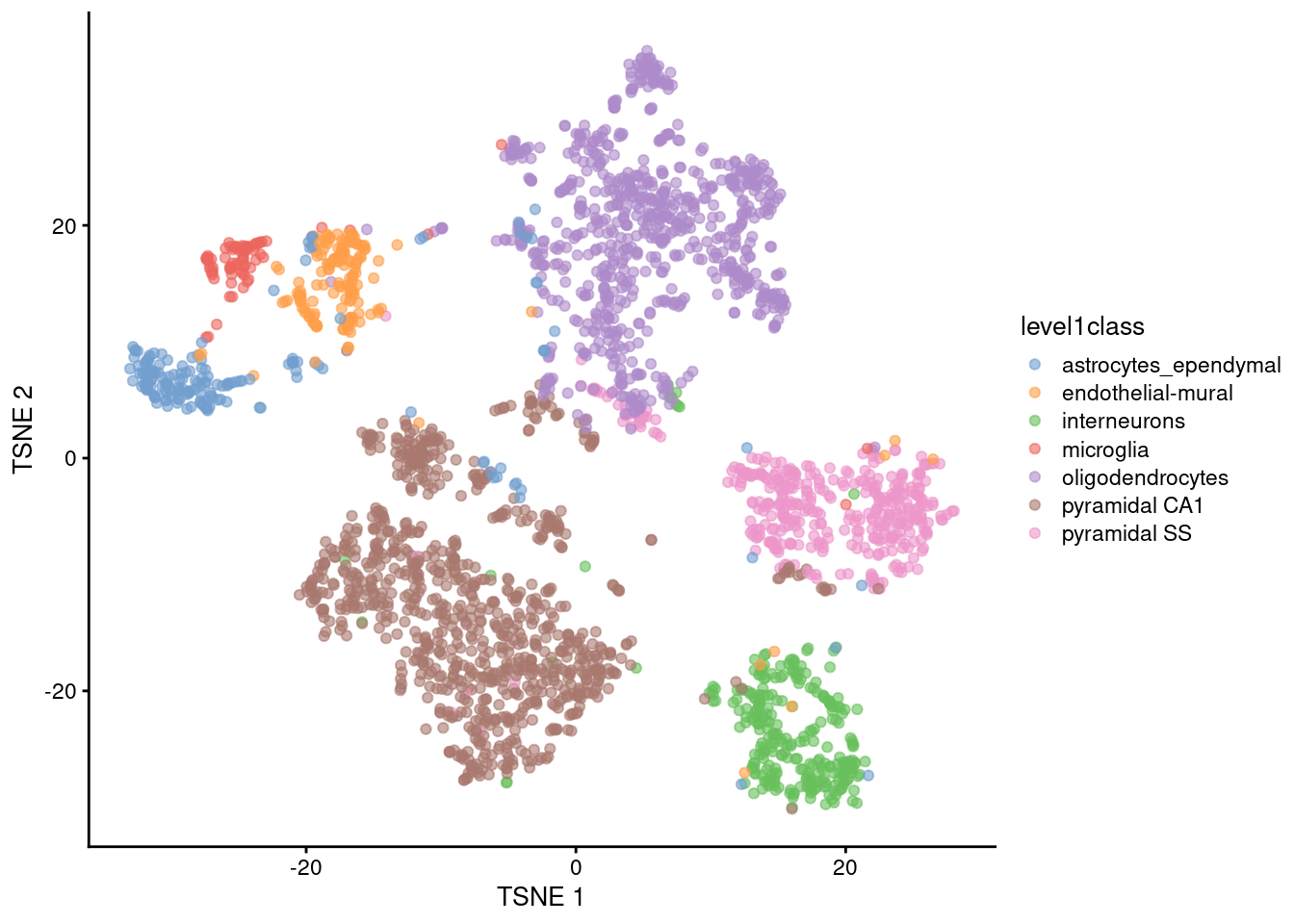
t-Distributed Stochastic Neighbor Embedding (t-SNE)
It has a stochastic step (results vary every time you run it)
Only local distances are preserved, while distances between groups are not always meaningful
Some parameters dramatically affect the resulting projection (in particular “perplexity”)
Learn more about how t-SNE works from this video: StatQuest: t-SNE, Clearly Explained
t-SNE
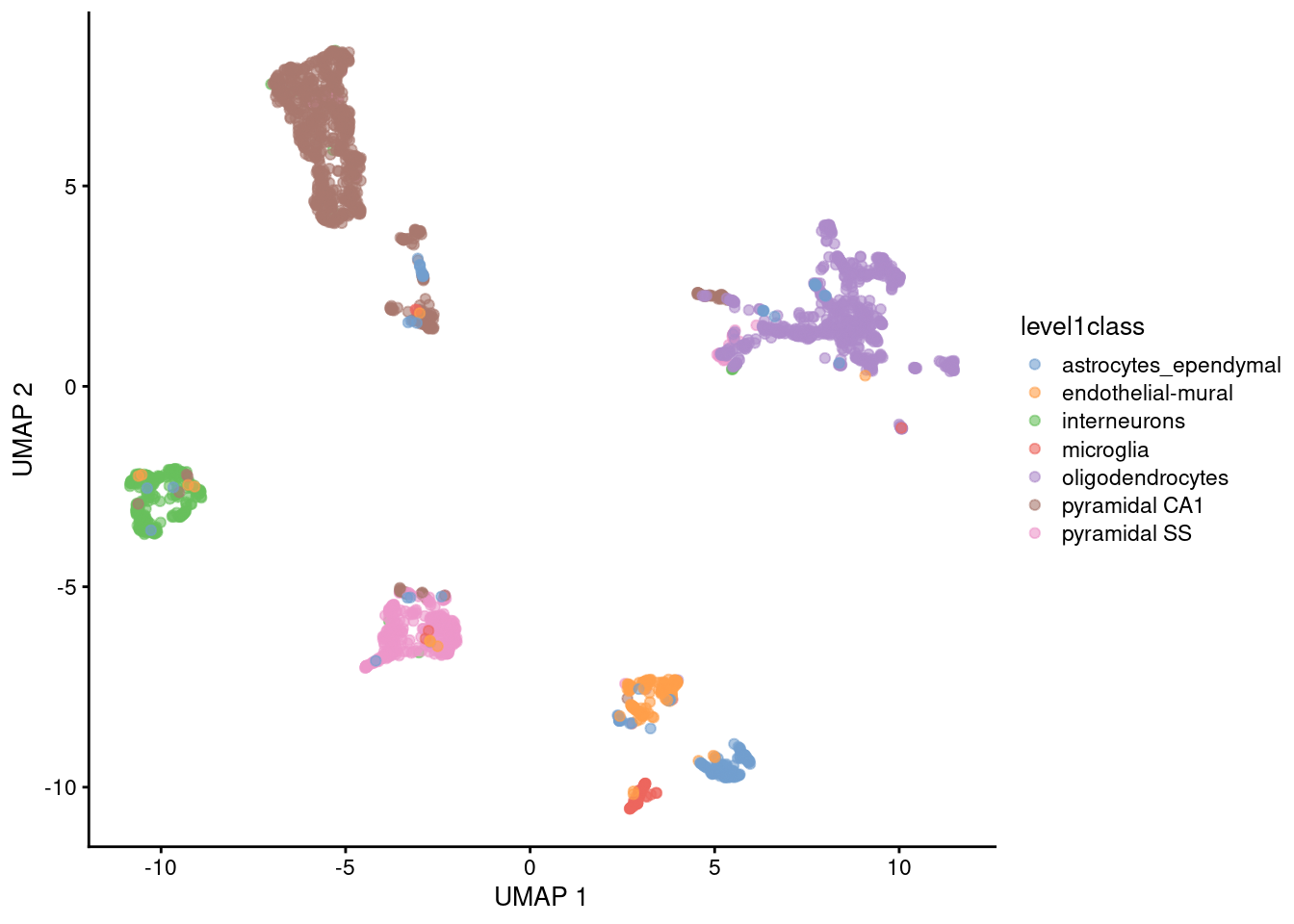
UMAP
Non-linear graph-based dimension reduction method like t-SNE
Newer & efficient = fast
Runs on top of PCs
Based on topological structures in multidimensional space
Unlike tSNE, you can compute the structure once (no randomization)
faster
you could add data points without starting over
Preserves the global structure better than t-SNE
UMAP
Key Points
- Dimensionality reduction methods allow us to represent high-dimensional data in lower dimensions, while retaining biological signal.
- The most common methods used in scRNA-seq analysis are PCA, t-SNE and UMAP.
- PCA uses a linear transformation of the data, which aims at defining new dimensions (axis) that capture most of the variance observed in the original data. This allows to reduce the dimension of our data from thousands of genes to 10-20 principal components.
- The results of PCA can be used in downstream analysis such as cell clustering, trajectory analysis and even as input to non-linear dimensionality reduction methods such as t-SNE and UMAP.
- t-SNE and UMAP are both non-linear methods of dimensionality reduction. They aim at keeping similar cells together and dissimilar clusters of cells apart from each other.
- Because these methods are non-linear, they should only be used for data visualisation, and not for downstream analysis.
Acknowledgments
Slides are adapted from Paulo Czarnewski and Zeynep Kalender-Atak
References (image sources):